

Implements an analog filter with transfer response specified by an arbitrary function.


Analog filters are generally specified by a rational polynomial. However there's no reason why this can't be generalized by allowing most any transfer function H(s). Use this filter for when you would like to use any H(s).
menu: veeos ==> Signal Processing ==> Modules ==> funcFilter
library: sigLib
Brickwall filter: The ultimate lowpass filter would remove all frequencies above a given limit. This is not realizable (is the limit of an infinite number of elements) but can certainly be modeled. For instance
H(s) = ( im(s) < 450 ? 1 : 0 ) would remove everything above 450Hz and allow everything below it to pass unimpeded
Phase shift: a pure phase shift is also not achievable in the real world except for at single frequency, but in the mathematical world is quite doable. In this case
H(s) = exp( S ) shifts the phase of everything by 90 degrees ( e^s becomes e^jF and hence 90 degree shift ).
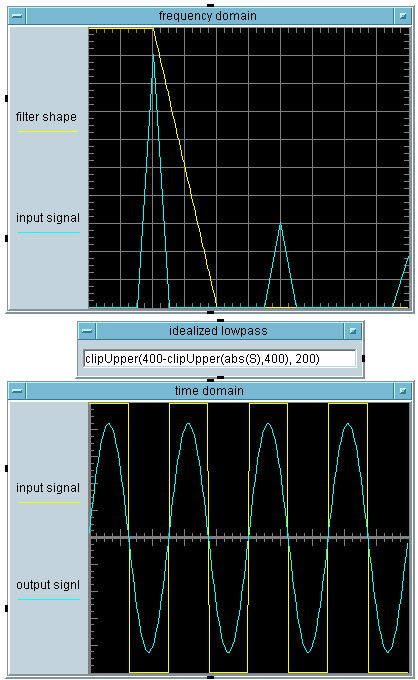
Rational polynomials are used for a very good reason to define filters: they are guaranteed to be stable (if poles are in LHP) , causal, and physically realizable. However there's nothing that says one can't use most any function to define the frequency response.
NOTE that the transfer function H(s) has a complex argument and that this filter filter operates on the jF axis (real frequencies) so any function that you write must be valid for complex numbers. Since some VEE functions do not support complex arguments you do need to be a little careful here.
VEE 7.0+, all platforms
aFilter, AnalogFilter, rootFilter, funcFilter